GRNPar: Parallel Inference of Gene Regulatory Networks Using Boolean Network Models and Mutual Information
Final project for COMS 4995 (Parallel Functional Programming, Fall 2022). Github repo here.
Introduction
Gene regulatory networks (GRNs) are graph-like representations of genes prone to activating or inhibiting the expression of other genes in a localized network. Boolean networks are often used to model GRNs—these networks consist of a series of nodes with connections between genes represented as boolean functions. Each node is a boolean variable that encodes its state (0 or 1). Each node’s state is determined by a boolean expression that takes as input the states of a subset of other nodes in the network. Researchers have developed algorithms for inferring these boolean expressions to model gene regulation activity.
For our project, we implemented a parallelized algorithm for inferring gene regulatory networks from gene expression time-series data using the boolean network model. Specifically, we modified a state-of-the-art approach put forth by Barman & Kwon (2017), which used a mutual information based approach coupled with a “swapping” subroutine to select dependent genes in the network and infer logical relations between input and output nodes.
In particular, we implemented and parallelized: (1) a mutual information approach for inferring depenencies in a boolean network, (2) boolean expressions mapping input nodes to output nodes, optimizing for a “gene-wise dynamics consistency” criterion, and a (3) method for visualizing and graphing the inferred boolean network. We parallelized each step, and specifically optimized key operations in the computation of possible boolean expressions that satisfy the various gene expression interactions in the network, where we saw the most speed-up.
Boolean Networks
The boolean network model G(V, A) proposed by Barman \&\ Kwon consists of nodes: \(V = \{v_1, ..., v_n\}\) and a set of interactions, or directed edges between input and output nodes: \(A = \{(v_i, v_j) \mid v_i, v_j \in V\}\), where \(v_j\) is a target node whose state depends on that of \(v_i\).
We further extend this model to account for boolean logic between the inferred input nodes and output nodes.
GRNPar Algorithm
Overview
We infer gene regulatory networks from time-series data by:
- First, finding the k input nodes with the highest mutual information in relation to every target node.
- Second, finding an optimal boolean expression that takes the k inferred input nodes with the highest dynamics criterion with respect to the target node. We choose the expression among a combination of \(2^{k-1}\) possible boolean expressions.
We also plot the inferred network to visualize our results as a final feature.
To determine the k most “closely related” input nodes for each node in the network, we used a mutual inference feature selection (MIFS) method based on entropy values (2.2.1). The testing of boolean expressions consists of finding possible boolean expressions which can be evaluated using the top k input nodes mapping to each target node, and choosing the one with highest gene-wise dynamics consistency (2.2.2).
Let V = \(\{\mathbf{v_0}, \mathbf{v_1}, ..., \mathbf{v_n}\}\) where each vector \(\mathbf{v_i}\) corresponds to a gene and \(\mathbf{v_i}(t)\) corresponds to its value, 0 or 1, at time t.

v0 in getOptimalBoolExpressions corresponds to a target node—given the network and connections generated, we iterate through each node and test for boolean expressions of its top k input nodes.
Finally, we plot the network as a directed graph, and return the inferred network, optimal boolean expressions for each node, and the image.
Criterions
Mutual Information
The mutual information metric used in Algorithm 2, \(I(X;Y)\), is based on the entropy of two variables. First, the entropy \(H(X)\) of a discrete random variable (gene) X is defined to measure the uncertainty of X over all time steps. A joint entropy \(H(X,Y)\) between \(X\) and \(Y\) measures the joint probability distribution between X and Y. The mutual information metric is then calculated based on these two entropy values.
Gene-wise Dynamics Consistency
Given the length of the time-series \(T\), and the observed and inferred boolean states of a node \(v\) and \(v'\) across a time-series, respectively, the gene-wise dynamics consistency is:
\begin{equation} E(v, v’) = \dfrac{\sum\limits^{T}_{t=2} I(v(t) = v’(t))}{T-1} \end{equation}
where \(I(v(t) = v'(t))\) here is equal to 1 if the condition \(v(t) = v'(t)\) is true, and 0 if false. \(v'(t)\) is obtained from a possible boolean expression that maps the inferred input nodes at time t with the target node at \(v'(t)\).
In essence, this criterion exposes the proportion of nodes whose states are predicted correctly given a boolean expression that outputs \(v'(t)\) at every timestep in the series. We used this criterion to choose an optimal boolean expression that maps the states of inferred input nodes to a target node.
searchUpdateRule
The searchUpdateRule function in src/BDDUtils.hs we implemented is where we search for possible boolean expressions that can be evaluated using the top k input nodes for each target node.
The authors from the original study included a second subroutine that iteratively swaps the selected k nodes with unselected nodes to see if different input nodes could yield higher dynamics consistency metrics—in their algorithm, the resulting number of input nodes could be less than or equal to k—whereas our implementation, due to time constraints, does not implement this swapping routine and selects a fixed k input nodes for each target node.
The essence of their swapping routine was a “search_update_rule” that searched through possible boolean expressions between the selected input nodes and updated the rule for each target node with the boolean expression that yielded the highest dynamics consistency. Our implementation of this lies in getOptimalBoolExpressions (Algorithm 3).


Haskell Implementation
Data Types
NodeState
NodeState represents the states of each node across the time-series. It consists of a String attribute as the name of the node/gene, and an [Int] to represent the boolean states/expression of that particular node across the time-series from time 1..T, where T is the length of the time-series.
BoolEdge
BoolEdge consists of two NodeState attributes—\(v\_i\) and \(v\_j\), which represents a directed edge dependency in the network from node \(v\_i\) to \(v\_j\).
BoolNetwork
BoolNetwork represents a boolean network as a directed graph. It contains a an attribute of [NodeState] consisting of the different nodes and their states across the time series, and an attribute of [BoolEdge] to represented the directed edges.
BDD
BDD is a recursive data type similar to a binary decision diagram. We created a variation to represent and evaluate boolean expressions. BDD consists of several different states:
- Name String: Represents the name of a particular boolean variable.
- State Int: Represents the state, 1 or 0, of a particular boolean variable.
- AND BDD BDD: Represents an AND logical operation between two BDD types.
- OR BDD BDD: Represents an OR logical operation between two BDD types.
- XOR BDD BDD: Represents an XOR logical operation between two BDD types.
- NOT BDD: Represents a NOT operation to be applied to a BDD.
The idea with BDD is to map out a boolean expression specifying variable names, and supply a [(String, Int)] which consists of Int boolean values for each variable name to a BDD data type that can evaluate the expression—evaluateFunc in src/BDDUtils.hs performs this task, like so:
-- Define a boolean expression with variable names x, y, a, z:
f = XOR (AND (Name "x") (OR (Name "y") (Name "a"))) (NOT (Name "z"))
-- Evaluate function by supplying values for each variable:
fromEnum $ evaluateFunc f [("x", 1), ("y", 0), ("a", 1), ("z", 1)]
This outputs 1 when evaluated. For simplicity, based on the original algorithm, we only look at a combination of conjunctive and disjunctive operations (AND/OR) evaluated using the the top k input nodes, sorted in descending order based on each node’s mutual information in relation to the target node.
Generating Random Time-Series Data
We generate random time series gene expression data in src/generate_data.py, which takes as input the number of nodes and timesteps—boolean states are randomly generated at each timestep.
Code Analysis
Mutual Information
First, we find the top k input nodes for each node in genBoolEdgesSeq, combining it into one list of BoolEdge and creating a BoolNetwork with the observed nodeStates and all of the generated BoolEdge connections (set of interactions).
genNetworkSeq :: [NodeState] -> Int -> BoolNetwork
genNetworkSeq nodeStates k = BoolNetwork nodeStates (combineEdgesSeq nodeStates k)
combineEdgesSeq :: [NodeState] -> Int -> [BoolEdge]
combineEdgesSeq nodeStates k = concatMap (genBoolEdgesSeq nodeStates k) nodeStates
genBoolEdgesSeq :: [NodeState] -> Int -> NodeState -> [BoolEdge]
genBoolEdgesSeq nodeStates k targetNode =
let topKMutual = getMutualInfoSeq targetNode (filter (/= targetNode) nodeStates) k
in map (`BoolEdge` targetNode) topKMutual
Extracting Optimal Boolean Expressions
Next, we determine the optimal boolean expressions (getOptimalBoolExpressions - line 223 BDDUtils.hs) for each input node. Using the boolNetwork and top k connections generated for each node, we generate a set of \(2^{k-1}\) possible boolean expressions and use each expression to infer a time-series to compare with the observed expressions of each node and calculate the gene-wise dynamics consistency (searchUpdateRule - line 169 BDDUtil.hs).
For each boolean expression, we take the state of each target node from time 2 to time T, and infer its value at every timestep t by evaluating the expression using the states of the selected k input nodes at time t-1. Using the inferred time series expression for the target node, we compare it with observed time series expression for the target node, and calculate the dynamics consistency. We choose the boolean expression that maximizes the genewise dynamics consistency for each target node, and assign that expression to it.
Lastly, we plot the BoolNetwork using the Data.Graph.DGraph library and graphviz library.
plotBoolNetworkPng :: BoolNetwork -> FilePath -> Bool -> IO FilePath
plotBoolNetworkPng network fname labelEdges = plotDGPng networkDG fname labelEdges
where
networkDG = boolNetworkToDG network labelEdges
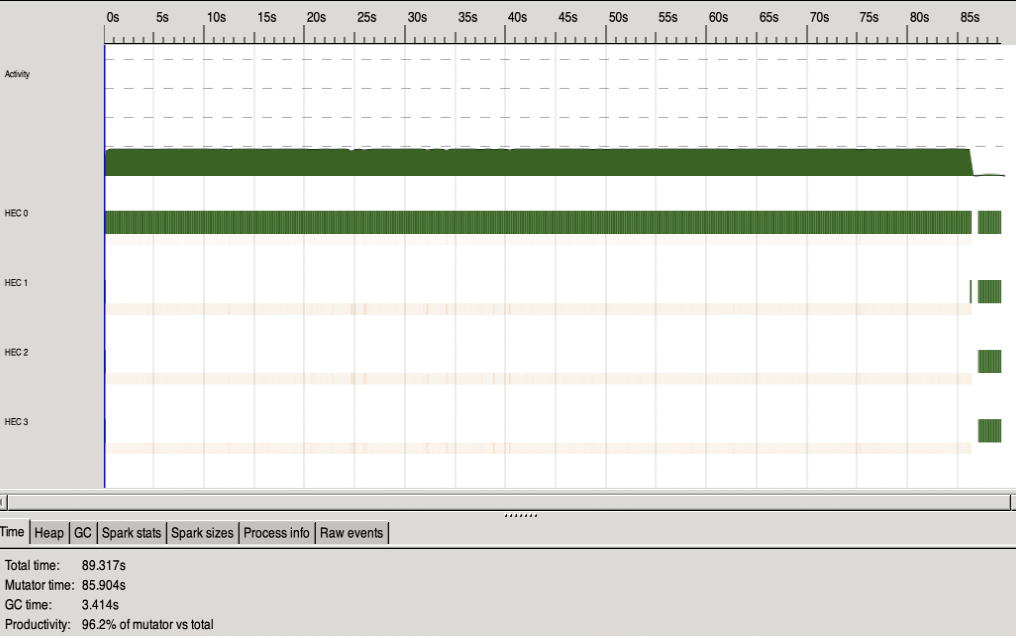
Figure 1: Sequential program for a randomized sample where 300 nodes are generated for 300 time steps and k=5.
Parallel Solution
We used genNetworkPar, getOptimalBoolExpressionsPar, and plotBoolNetworkPngPar in Main.hs to run parallel strategies. We made NFData instances for NodeState, BoolEdge, and BoolNetwork to perform these computations.
There are three layers of parallelism applied to the implementation to improve the performance of the program. The first layer uses the parMap deepSeq functions from the package Control.Parallel.Strategies. The second and third layer use parBuffer and parChunkList, respectively.
We used parMap rdeepseq to parallelize map computations. We used parMap to combine the results of generating the top k connections into one list, shown in the new combineEdgesPar function in GRNPar.hs. Similarly, when parsing through all the possible nodes to determine the top k nodes based on mutual information, we applied parMap rdeepseq and ran the calculations in parallel.
allMutualInfo =
map (\inp ->
(inp, mutualInformation (timeStates inp) (timeStates targetNode)
- sum (parMap rdeepseq (mutualInformation (timeStates inp) . timeStates)
$ map fst regNodes))) inpNodes `using` parBuffer 3 rdeepseq
Here, we use parBuffer to iterate through the input nodes and calculate mutual information.
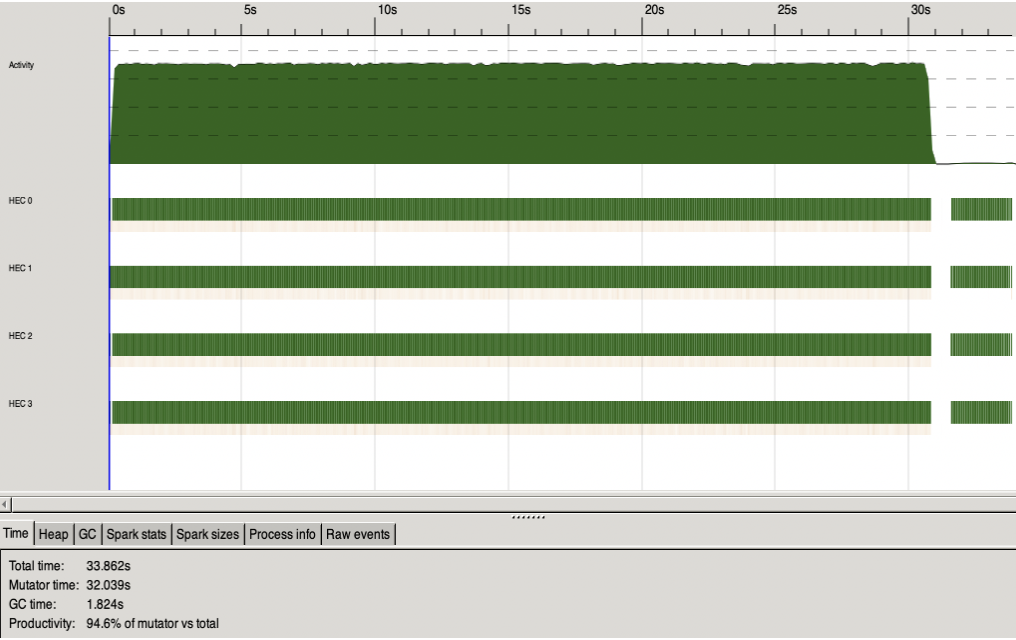
Figure 2. Parallel program for a randomized sample where 300 nodes are generated for 300 time steps and k=5.
Figure 2 shows the eventlog when running parallel on a randomly generated time-series containing 300 nodes and 300 timesteps. The test was run on 4 cores with k = 5. The average runtime was 33.9 seconds.
Performance Analysis
Results
Real-world Datasets
We tested GRNPar with three real gene expression datasets: an E. coli network with 10 genes and 20 timesteps, an Insilico E.coli network with 100 genes and 20 timesteps, and a fission yeast cell cycle network with 10 genes and 10 timesteps. We discretized the InSilico data using a rudimentary KMeans clustering algorithm, and the other datasets had been discretized to boolean states using KMeans clustering prior by Barman & Kwon.
We ran the Insilico E. coli dataset through GRNPar, only generating the network without computing expressions or outputting an image, both in parallel and sequentially—the results are shown in Figure 3. There was a 2.16x speedup in total time and 2.25x reduction in mutator time from the sequential to parallel run.
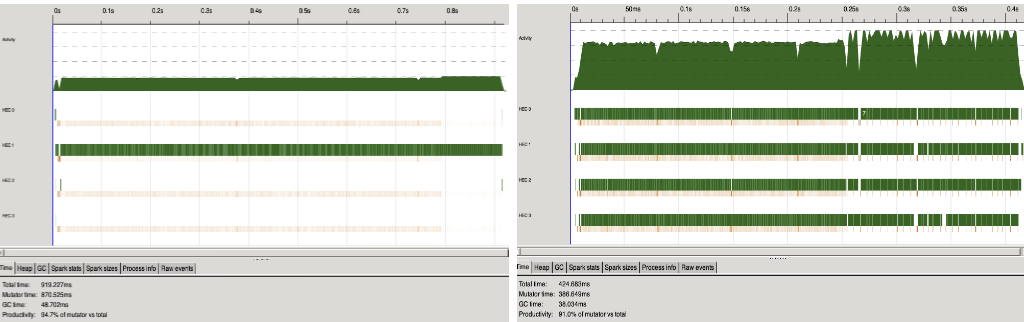
Figure 3. Sequential (left) and Parallel (right) program for GRNPar on Insilico E. coli Dataset using 4 cores. k = 8.
When running the Insilico data through GRNPar, there was an extra period for generating the image, in both the sequential and parallel versions of the algorithm. This is seen in the extra time taken to complete the algorithm in Figure 4. In both the sequential and parallel algorithms, it took 1.5 seconds extra to run as compared with the runs when the graph image was not generated.
The graph generated for the Insilico set is shown in figure 5. There is a tendency for the central nodes to be in the center of the graph, as they have more dependencies. Figure 6 shows the graphs generated by testing GRNPar on the other E. coli dataset and fission yeast cell cycle network-similar to the Insilico set, we observe 3.33x speedup between the sequential and parallel usage of GRNPar.
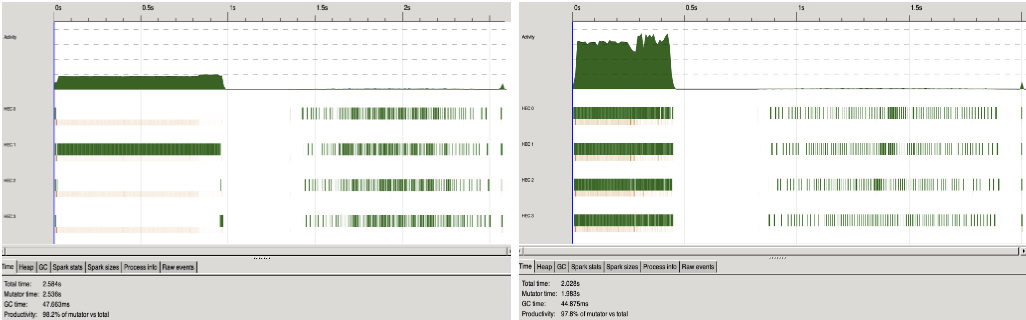
Figure 4. Generation of network + plotting image -> both the sequential (left) and parallel (right) implementation took ~1.5 extra seconds, compared to Figure 3.
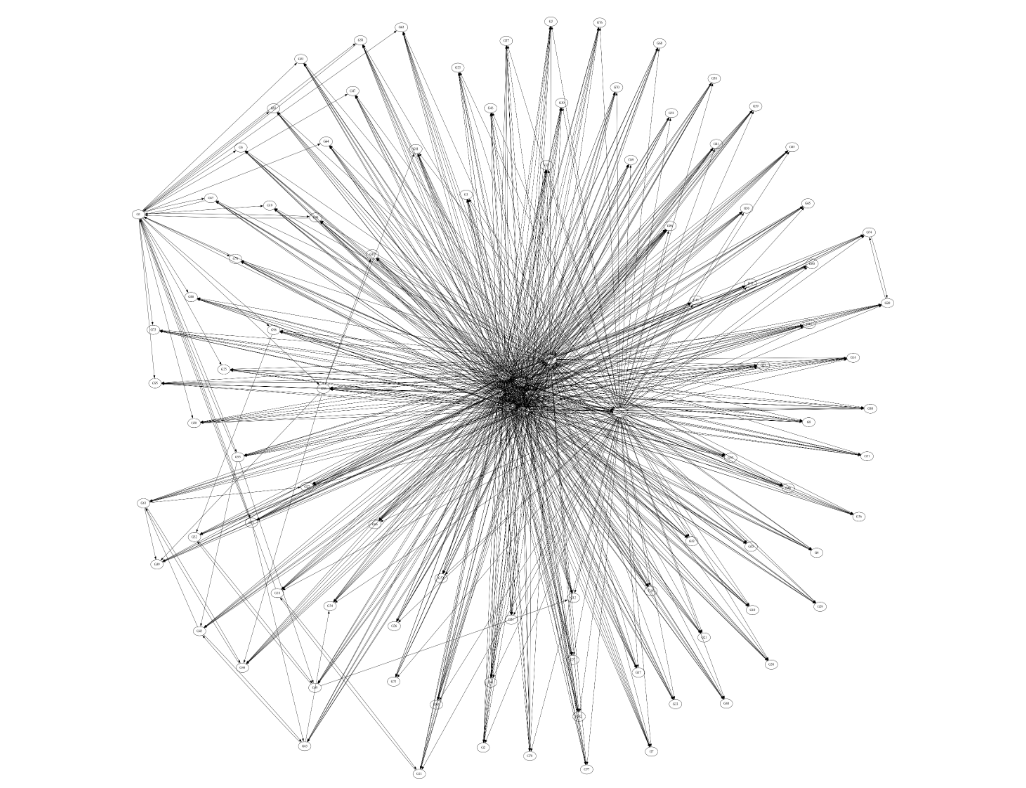
Figure 5. Boolean Network Inferred for InSilico Ecoli Protein Trajectories
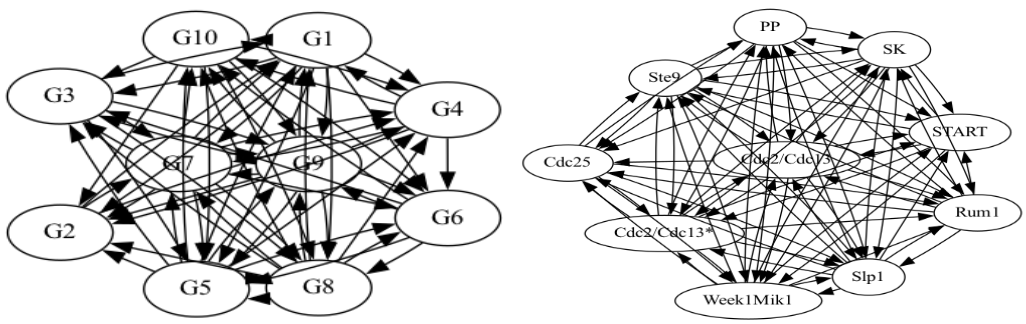
Figure 6. E. coli gene regulatory network(left) \&\ a fission yeast cell cycle network (right).
Randomly Generated Data
We also analyzed how changing the number of nodes (genes), cores, and k-values affected performance of GRNPar on randomly generated time-series expression data. Figure 8 shows three tables worth of runtime data. In Table 1, as the number of nodes (genes) increases, the runtime for sequential GRNPar increases at a much larger rate than parallel GRNPar. However, when compared with the parallel runtime in Table 2 (Figure 8), the sequential runtime increases as the number of cores increases, since unnecessary garbage collection occurs during the sequential run as more cores are added on.
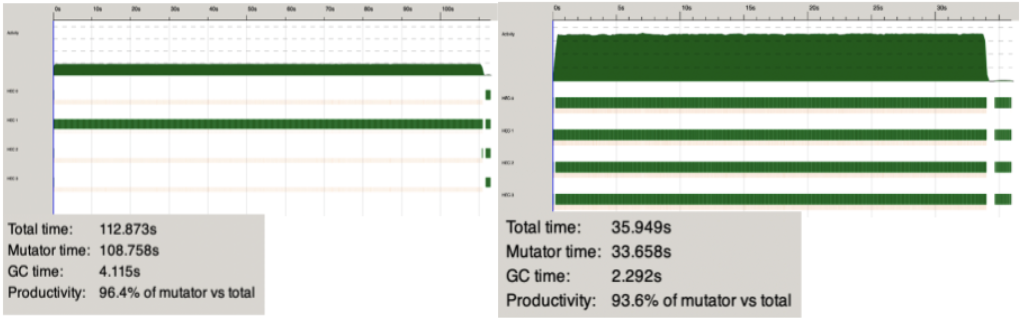
Figure 7. Randomly Generated Data: 500 Nodes over 300 time steps (4 cores) in a sequential and parallel method.
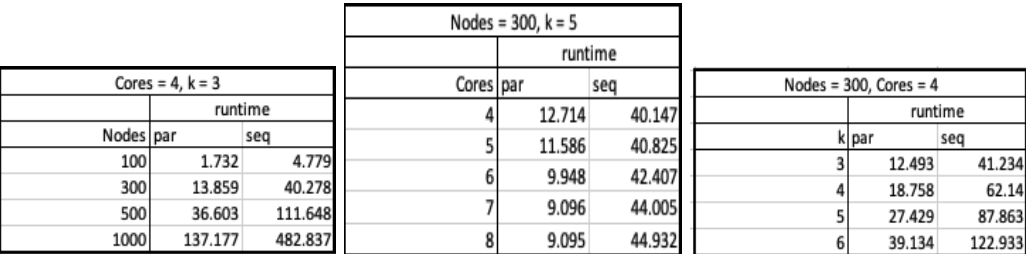
From left to right, Table 1, 2, 3. Table 1: Change in runtime for a parallel and sequential implementation as the number of nodes increases. Table 2: Change in runtime for a parallel and sequential implementation as the number of cores increases. Table 3: Change in runtime for a parallel and sequential implementation as the k value increases.
Running GRNPar
This program takes in five arguments:
stack exec GRNPar-exe <csvFilename> <k> <genExpressions> <genImage> <mode>
Specific implementation details can be found in the README. The output of the program is a .png file that has the boolean network mapped out in src/output_files.
References
Barman S, Kwon YK (2017) A novel mutual information-based Boolean network inference method from time-series gene expression data. PLOS ONE 12(2): e0171097.\https://doi.org/10.1371/journal.pone.0171097
Prill RJ, Marbach D, Saez-Rodriguez J, Sorger PK, Alexopoulos LG, Xue X, et al. Towards a Rigorous Assessment of Systems Biology Models: The DREAM3 Challenges. PLOS One.
Code Listing
app/Main.hs
{-
Main application program:
-}
module Main (main) where
import System.IO ()
import System.Environment (getArgs)
import Control.Monad
import GRNPar (genNetworkSeq, genNetworkPar)
import GraphUtils (plotBoolNetworkPng, plotBoolNetworkPngPar, NodeState(..))
import BDDUtils (getOptimalBoolExpressions, getOptimalBoolExpressionsPar)
import ProcessData (csvToNodeStates)
import Control.DeepSeq
{-
Main script:
1. Infer + generate boolean network from input file
2. Determine optimal boolean expression
3. Output network to png file
Usage: GRNPar-exe <csvFilename> <k> <outputFile> <genExpressions> <genImage> <mode>
-}
main :: IO ()
main = do
args <- getArgs
case args of
[fname, k, genExpressions, genImage, mode] -> do
putStrLn fname
putStrLn "Parsing data..."
nodeStates@(x:_) <- csvToNodeStates fname 1
-- Generate network with dependencies
let k' = read k :: Int
timeLength = length $ timeStates x
network = if mode == "par"
then force $ genNetworkPar nodeStates k'
else force $ genNetworkSeq nodeStates k'
putStrLn "Generated network."
when (genExpressions == "1") $ do
-- Get optimal boolean expressions for each node
let optimalExpressions = if mode == "par"
then force $ getOptimalBoolExpressionsPar network timeLength
else force $ getOptimalBoolExpressions network timeLength
putStrLn "Optimal boolean expressions for each variable:"
mapM_ (\(n, b, c) -> putStrLn $ name n ++ " = " ++ show b ++ ". Gene-wise consistency: " ++ show c) optimalExpressions
--print optimalExpressions
when (genImage == "1") $ do
-- Print image
let outputFile = "src/output_files/" ++ substring (length "src/data/") (length fname - 4) fname
print outputFile
imgFilepath <- if mode == "par"
then plotBoolNetworkPngPar network outputFile False
else plotBoolNetworkPng network outputFile False
putStrLn $ "Printed to " ++ imgFilepath ++ "."
putStrLn "Finished."
_ -> putStrLn "Usage: GRNPar-exe <csvFilename> <k> <outputFile> <genExpressions> <genImage> <mode>"
substring :: Int -> Int -> String -> String
substring x y s = take (y - x) (drop x s)
src/GRNPar.hs
{-# LANGUAGE ParallelListComp #-}
module GRNPar
( genNetworkSeq
, genNetworkPar
) where
import Control.Monad ()
import qualified Data.Map as Map
import Data.Ord (comparing)
import Data.List (maximumBy, sortBy)
import GraphUtils (NodeState(..), BoolEdge(..), BoolNetwork(..))
import Control.Parallel.Strategies (parMap, rdeepseq, parBuffer, using)
import Control.DeepSeq ()
{-
-- Testing with sample nodes:
x_1 :: NodeState
x_1 = NodeState "x_1" [1, 1, 0, 0, 0, 1, 0, 1]
x_2 :: NodeState
x_2 = NodeState "x_2" [1, 0, 1, 0, 1, 0, 1, 0]
x_3 :: NodeState
x_3 = NodeState "x_3" [1, 0, 1, 0, 1, 0, 1, 0]
x_4 :: NodeState
x_4 = NodeState "x_4" [1, 0, 0, 0, 1, 0, 1, 1]
x_5 :: NodeState
x_5 = NodeState "x_5" [1, 0, 1, 0, 0, 0, 0, 0]
x_6 :: NodeState
x_6 = NodeState "x_6" [1, 1, 0, 0, 1, 1, 1, 0]
sampleNodes :: [NodeState]
sampleNodes = [x_1,x_2,x_3,x_4,x_5,x_6]
-}
{-
Parallel pipeline for inferring boolean network given NodeState data.
-}
genNetworkPar :: [NodeState] -> Int -> BoolNetwork
genNetworkPar nodeStates k = BoolNetwork nodeStates (combineEdgesPar nodeStates k)
{-
Sequential pipeline for inferring boolean network given NodeState data.
-}
genNetworkSeq :: [NodeState] -> Int -> BoolNetwork
genNetworkSeq nodeStates k = BoolNetwork nodeStates (combineEdgesSeq nodeStates k)
{-
Combine all BoolEdge connections for each target node into one array.
-}
combineEdgesSeq :: [NodeState] -> Int -> [BoolEdge]
combineEdgesSeq nodeStates k = concatMap (genBoolEdgesSeq nodeStates k) nodeStates
{-
Generate BoolEdge connections in network given NodeState and a targetNode
-}
genBoolEdgesSeq :: [NodeState] -> Int -> NodeState -> [BoolEdge]
genBoolEdgesSeq nodeStates k targetNode =
let topKMutual = getMutualInfoSeq targetNode (filter (/= targetNode) nodeStates) k
in map (`BoolEdge` targetNode) topKMutual
combineEdgesPar :: [NodeState] -> Int -> [BoolEdge]
combineEdgesPar nodeStates k = concat $ parMap rdeepseq (genBoolEdgesPar nodeStates k) nodeStates
genBoolEdgesPar :: [NodeState] -> Int -> NodeState -> [BoolEdge]
genBoolEdgesPar nodeStates k targetNode = map (`BoolEdge` targetNode) topKMutual
where
topKMutual = getMutualInfoPar targetNode (filter (/= targetNode) nodeStates) k
{-
Get top k input nodes with the highest mutual information relative to a target node.
Return input nodes sorted descending based on mutual information with target node.
* inputNodes should not contain targetNode when calling getMutualInfo
-}
getMutualInfoSeq :: NodeState -> [NodeState] -> Int -> [NodeState]
getMutualInfoSeq targetNode inputNodes k = map fst
$ sortBy (flip (comparing snd))
$ getMutualInfo' [maxMutualNodeInfo]
(filter (/= maxMutual) inputNodes) k
where
maxMutualNodeInfo@(maxMutual, _) = maximumBy (comparing snd)
$ map (\inp -> (inp, mutualInformation (timeStates inp) (timeStates targetNode))) inputNodes
getMutualInfo' :: [(NodeState, Double)] -> [NodeState] -> Int -> [(NodeState, Double)]
getMutualInfo' regNodes inpNodes k' -- regNodes -> regulatory nodes currently being examined
| length regNodes == k' = regNodes
| otherwise =
let newMaxInfo@(newMax, _) = maximumBy (comparing snd)
$ map (\inp -> (inp, mutualInformation (timeStates inp) (timeStates targetNode)
- sum (map (mutualInformation (timeStates inp) . timeStates) $ map fst regNodes))) inpNodes
newInpNodes = filter (/= newMax) inpNodes
newRegNodes = regNodes ++ [newMaxInfo]
in getMutualInfo' newRegNodes newInpNodes k'
getMutualInfoPar :: NodeState -> [NodeState] -> Int -> [NodeState]
getMutualInfoPar targetNode inputNodes k = map fst
$ sortBy (flip (comparing snd))
$ getMutualInfo' [maxMutualNodeInfo]
(filter (/= maxMutual) inputNodes) k
where
mutualInfo' = map (\inp -> (inp, mutualInformation (timeStates inp) (timeStates targetNode)))
inputNodes `using` parBuffer 3 rdeepseq
maxMutualNodeInfo@(maxMutual, _) = maximumBy (comparing snd) mutualInfo'
getMutualInfo' :: [(NodeState, Double)] -> [NodeState] -> Int -> [(NodeState, Double)]
getMutualInfo' regNodes inpNodes k'
| length regNodes == k' = regNodes
| otherwise =
let allMutualInfo = map (\inp -> (inp, mutualInformation (timeStates inp) (timeStates targetNode)
- sum (parMap rdeepseq (mutualInformation (timeStates inp) . timeStates) $ map fst regNodes)))
inpNodes `using` parBuffer 3 rdeepseq
newMaxInfo@(newMax, _) = maximumBy (comparing snd) allMutualInfo
newInpNodes = filter (/= newMax) inpNodes
newRegNodes = regNodes ++ [newMaxInfo]
in getMutualInfo' newRegNodes newInpNodes k'
-- Compute the entropy of a list of numerical values
entropy :: (Ord a) => [a] -> Double
entropy xs = sum [ -p * logBase 2 p | p <- ps ]
where
counts = Map.fromListWith (+) [(x, 1 :: Int) | x <- xs]
values = Map.elems counts
total = sum values
ps = [fromIntegral v / fromIntegral total | v <- values]
-- Compute the mutual information of discrete variables x and y
mutualInformation :: (Ord a) => [a] -> [a] -> Double
mutualInformation xs ys = entropy xs + entropy ys - entropy (zip xs ys)
src/GraphUtils.hs
module GraphUtils
( NodeState(..)
, BoolEdge(..)
, BoolNetwork(..)
, plotBoolNetworkPng
, plotBoolNetworkPngPar
, plotDGPng
) where
import Data.GraphViz
import Data.GraphViz.Attributes.Complete
import Data.Hashable
import Control.Parallel.Strategies (parListChunk, rdeepseq, using)
import Control.DeepSeq ( NFData(..) )
import qualified Data.Text.Lazy as TL
import qualified Data.Graph.DGraph as DG
import qualified Data.Graph.Types as GT
{-
Data types representing boolean states of genes and boolean network consisting of NodeStates and directed edges.
- NodeState:
- name :: String -> name of gene
- timeStates :: [Int] -> expression of gene across time-series in order
-}
data NodeState = NodeState { name :: String
, timeStates :: [Int] } deriving (Eq, Ord)
instance Show NodeState where
show (NodeState n _) = n
instance NFData NodeState where
rnf (NodeState n ts) = rnf n `seq` rnf ts
{-
- BoolEdge
- v_i :: NodeState -> source node
- v_j :: NodeState -> target node
-}
data BoolEdge = BoolEdge { v_i :: NodeState
, v_j :: NodeState } deriving (Eq)
instance Show BoolEdge where
show (BoolEdge i j) = "(" ++ name i ++ " -> " ++ name j ++ ")"
instance NFData BoolEdge where
rnf (BoolEdge i j) = rnf i `seq` rnf j
{-
- BoolNetwork
- nodes :: [NodeState] -> all nodes/genes in network
- connections :: [BoolEdge] -> directed edges between genes
-}
data BoolNetwork = BoolNetwork { nodes :: [NodeState]
, connections :: [BoolEdge] } deriving (Eq, Show)
instance NFData BoolNetwork where
rnf (BoolNetwork n c) = rnf n `seq` rnf c
{-
Modified from graphite lib source code:
- Functions for plotting directed graph and BoolNetwork to png file
- graphviz needs to be installed on local machine to see output:
- brew install graphviz
OR
- sudo apt install graphviz
Example: Plot DGraph foundationUniverse to "foundation.png"
foundationUniverse :: DG.DGraph String Double
foundationUniverse = DG.fromArcsList
[ GT.Arc "Helicon" "Nishaya" 200.00
, GT.Arc "Helicon" "Wencory" 382.20
, GT.Arc "Nishaya" "Wencory" 820.32
]
plotDGraphPng foundationUniverse "foundation"
-}
-- Plot a BoolNetwork to png file
boolNetworkToDG :: BoolNetwork -> Bool -> DG.DGraph String String
boolNetworkToDG network labelEdges = DG.fromArcsList
$ map (\(BoolEdge inp out) ->
GT.Arc (name inp) (name out) (if labelEdges then "test" else ""))
(connections network)
-- Plot a BoolNetwork to png file
boolNetworkToDGPar :: BoolNetwork -> Bool -> DG.DGraph String String
boolNetworkToDGPar network labelEdges = DG.fromArcsList
(map (\(BoolEdge inp out) ->
GT.Arc (name inp) (name out) (if labelEdges then "test" else ""))
(connections network)
`using` parListChunk 50 rdeepseq)
-- Plot BoolNetwork to png file
plotBoolNetworkPng :: BoolNetwork -> FilePath -> Bool -> IO FilePath
plotBoolNetworkPng network fname labelEdges = plotDGPng networkDG fname labelEdges
where
networkDG = boolNetworkToDG network labelEdges
plotBoolNetworkPngPar :: BoolNetwork -> FilePath -> Bool -> IO FilePath
plotBoolNetworkPngPar network fname labelEdges = plotDGPng networkDG fname labelEdges
where
networkDG = boolNetworkToDGPar network labelEdges
-- | Plot a directed 'DGraph' to a PNG image file
plotDGPng :: (Hashable v, Ord v, PrintDot v, Show v, Show e)
=> DG.DGraph v e
-> FilePath
-> Bool
-> IO FilePath
plotDGPng g fname labelEdges = addExtension (runGraphvizCommand Sfdp $ toDirectedDot labelEdges g) Png fname
labeledNodes :: (GT.Graph g, Show v) => g v e -> [(v, String)]
labeledNodes g = (\v -> (v, show v)) <$> GT.vertices g
labeledArcs :: (Hashable v, Eq v, Show e) => DG.DGraph v e -> [(v, v, String)]
labeledArcs g = (\(GT.Arc v1 v2 attr) -> (v1, v2, show attr)) <$> DG.arcs g
toDirectedDot :: (Hashable v, Ord v, Show v, Show e)
=> Bool -- ^ Label edges
-> DG.DGraph v e
-> DotGraph v
toDirectedDot labelEdges g = graphElemsToDot params (labeledNodes g) (labeledArcs g)
where params = sensibleDotParams True labelEdges
sensibleDotParams
:: Bool -- ^ Directed
-> Bool -- ^ Label edges
-> GraphvizParams t l String () l
sensibleDotParams directed edgeLabeled = nonClusteredParams
{ isDirected = directed
, globalAttributes =
[ GraphAttrs [Overlap ScaleOverlaps]
, EdgeAttrs [FontColor (X11Color DarkGreen)]
]
, fmtEdge = edgeFmt
}
where
edgeFmt (_, _, l) = if edgeLabeled
then [Label $ StrLabel $ TL.pack l]
else []
src/BDDUtils.hs
{-# LANGUAGE TupleSections #-}
module BDDUtils
( BDD(..)
, evaluateFunc
, getOptimalBoolExpressions
, getOptimalBoolExpressionsPar
, getRegulatoryNodes
, searchUpdateRule
, getBDDFromFunc
) where
import GraphUtils (NodeState(..), BoolEdge(..), BoolNetwork(..))
import Data.Ord (comparing)
import Data.List (maximumBy)
import qualified Data.Matrix as M
import qualified Data.Vector as Vec
import Control.Parallel.Strategies (parMap, rdeepseq, using, parListChunk, parBuffer)
import Control.DeepSeq(NFData(..))
{-
Functions for evaluating and representing binary decision diagrams.
-}
{-
Binary decision diagram data type used for evaluating boolean expressions.
Example:
- f = XOR (AND (Name "x") (OR (Name "y") (Name "a"))) (NOT (Name "z"))
- fromEnum $ evaluateFunc f [("x", 1), ("y", 0), ("a", 1), ("z", 1)]
- Output: 1
-}
-- Define binary decision diagram
data BDD = Name String -- name of node (gene name)
| State Int -- state of node (0 or 1)
| AND BDD BDD -- an AND node
| OR BDD BDD -- an OR node
| XOR BDD BDD -- an XOR node
| NOT BDD -- a NOT node
deriving (Eq)
instance Show BDD where
show (Name x) = x
show (State x) = show x
show (AND x y) = "(" ++ show x ++ " AND " ++ show y ++ ")"
show (OR x y) = "(" ++ show x ++ " OR " ++ show y ++ ")"
show (XOR x y) = "(" ++ show x ++ " XOR " ++ show y ++ ")"
show (NOT x) = "(NOT " ++ show x ++ ")"
instance NFData BDD where
rnf (Name x) = rnf x
rnf (State x) = rnf x
rnf (AND x y) = rnf x `seq` rnf y
rnf (OR x y) = rnf x `seq` rnf y
rnf (XOR x y) = rnf x `seq` rnf y
rnf (NOT x) = rnf x
{-
Evaluate a boolean expression given a BDD data type and a list of tuples specifying values for each variable.
Params:
- BDD data type
- func: list of tuples [(varName, value)], where varName is a boolean variable name in the BDD, and value is the value assigned to it
Example:
- f = XOR (AND (Name "x") (OR (Name "y") (Name "a"))) (NOT (Name "z"))
- fromEnum $ evaluateFunc f [("x", 1), ("y", 0), ("a", 1), ("z", 1)]
- Output: 1
-}
-- evaluate a BDD for a given assignment of the variables
evaluateFunc :: BDD -> [(String, Int)] -> Bool
evaluateFunc (Name x) func = case lookup x func of
Just a -> a == 1
Nothing -> error "Variable not in assignment"
evaluateFunc (AND x y) func = evaluateFunc x func && evaluateFunc y func
evaluateFunc (OR x y) func = evaluateFunc x func || evaluateFunc y func
evaluateFunc (XOR x y) func
| andTrue = False
| otherwise = evaluateFunc (OR x y) func
where
andTrue = evaluateFunc x func && evaluateFunc y func
evaluateFunc (NOT b) func = not (evaluateFunc b func)
evaluateFunc (State x) _
| x == 1 = True
| otherwise = False
{-
Get gene wise dynamics consistency metric given a predicted time series and the actual time series.
Params:
- predictedStates :: [Int]
- actualStates :: [Int]
-}
geneWiseDynamicsConsistency :: [Int] -> [Int] -> Double
geneWiseDynamicsConsistency predictedStates actualStates = sumPredictions / fromIntegral timeLength
where
sumPredictions = sum $ zipWith (\x y -> if x == y then 1 :: Double else 0 :: Double) predictedStates actualStates
timeLength = length predictedStates
{-
Get all combinations of conjunctive and disjunctive boolean expressions.
Params:
- n :: Int -> number of operators to evaluate
Returns:
- [[Int]] -> list of Int lists, where each list corresponds to a sequence of AND/OR operations.
Each list, e.g. [1, 0, 1], signifies a sequence of AND/OR operators, where 1 = AND and 0 = OR
Example: given a list of truth values, such as [1, 0, 0, 1], and a boolean expression combination represented as [1, 0, 1]:
- Using the BDD data type, we would evaluate this as: ((1 AND 0) OR 0) AND 1
-}
getConjDisjCombos :: Int -> [[Int]]
{-
getConjDisjCombos 1 = [[0], [1]]
getConjDisjCombos n = [[mod x 2^i | i <- [0..n-1]] | x <- [0..(2^n)-1]]
-}
getConjDisjCombos 0 = [[]]
getConjDisjCombos n = [(x:xs) | x <- [0, 1], xs <- getConjDisjCombos (n-1)]
{-
Construct a BDD given boolean variable names and a combination of conjunctive/disjunctive operations.
Params:
- (x:xs) :: [String] -> boolean variable names
- ops :: [Int] -> conjunctive/disjunctive combinations as one element outputted by getConjDisjCombos
Returns: BDD
The number of variables should always be 1 more than the number of operations.
Example:
- getBDDFromFunc ["v1", "v2", "v3"] [1, 0] returns a BDD of: ((v1 AND v2) OR v3)
- bdd = getBDDFromFunc ["v1", "v2", "v3"] [1, 0]
- fromEnum $ evaluateFunc bdd [("v1", 1), ("v2", 0), ("v3", 1)]
- Output: 1
-}
getBDDFromFunc :: [String] -> [Int] -> BDD
getBDDFromFunc [] _ = error "Invalid input."
getBDDFromFunc [_] _ = error "Invalid input."
getBDDFromFunc (x:xs) ops = foldl (\acc (y, ys) -> if ys == 1 then AND acc (Name y) else OR acc (Name y)) (Name x) tailZipped
where
tailZipped = zip xs ops
{-
Get regulatory genes of node given target node and boolean network.
Params:
- targetNode: target gene
- network : BoolNetwork
-}
getRegulatoryNodes :: NodeState -> BoolNetwork -> [NodeState]
getRegulatoryNodes targetNode network = map v_i $ filter (\(BoolEdge _ out) -> out == targetNode) $ connections network
{-
Compute genewise dynamics consistency metric for possible boolean expressions in input nodes sorted by mutual information.
Params:
- inpNodes :: [NodeState] -> top k input nodes with highest mutual information with respect to targetNode
- targetNode :: NodeState
- timeLength :: Int -> length of time series
-}
searchUpdateRule :: [NodeState] -> NodeState -> Int -> [(Double, BDD)]
searchUpdateRule inpNodes targetNode timeLength =
case allTargetStates of
[] -> error "Invalid target states."
[_] -> error "Invalid target states."
(_:targetStates) -> map (\(p, r) -> (geneWiseDynamicsConsistency p targetStates, r)) predStates
where
-- Get target states of target node
allTargetStates = timeStates targetNode
inpNodeNames = map name inpNodes
inpMatrix = M.fromLists $ map (\xs -> map (name xs,) (timeStates xs)) inpNodes
-- Get boolean expression combos
ruleCombos = map (getBDDFromFunc inpNodeNames) $ getConjDisjCombos (length inpNodes - 1)
-- Predict states using boolean expression
predStates = map (\ruleBDD ->
let p = map (fromEnum . \t -> evaluateFunc ruleBDD (filter (\(nn, _) -> nn `elem` inpNodeNames)
$ Vec.toList (M.getCol t inpMatrix)))
[1..(timeLength - 1)]
in (p, ruleBDD))
ruleCombos
searchUpdateRulePar :: [NodeState] -> NodeState -> Int -> [(Double, BDD)]
searchUpdateRulePar inpNodes targetNode timeLength =
case allTargetStates of
[] -> error "Invalid target states."
[_] -> error "Invalid target states."
(_:targetStates) -> map (\(p, r) -> (geneWiseDynamicsConsistency p targetStates, r)) predStates
where
-- Get target states of target node
allTargetStates = timeStates targetNode
inpNodeNames = map name inpNodes
inpMatrix = M.fromLists $ map (\xs -> map (name xs,) (timeStates xs) `using` parBuffer 50 rdeepseq) inpNodes
-- Get boolean expression combos
ruleCombos = map (getBDDFromFunc inpNodeNames) (getConjDisjCombos (length inpNodes)) `using` parBuffer 100 rdeepseq
-- Predict states using boolean expression
predStates = parMap rdeepseq (\ruleBDD ->
let p = map (fromEnum . \t -> evaluateFunc ruleBDD (filter (\(nn, _) -> nn `elem` inpNodeNames)
$ Vec.toList (M.getCol t inpMatrix)))
[1..(timeLength - 1)]
`using` parBuffer 50 rdeepseq
in (p, ruleBDD))
ruleCombos
{-
Get optimal boolean expressions for each node in network that optimizes genewise dynamics consistency.
-}
getOptimalBoolExpressions :: BoolNetwork -> Int -> [(NodeState, BDD, Double)]
getOptimalBoolExpressions inferredNetwork timeLength = map (\targetNode ->
let inpNodes = getRegulatoryNodes targetNode inferredNetwork
-- Get consistency metrics for each boolean expression
consistencyMetrics = searchUpdateRule inpNodes targetNode timeLength
-- Get boolean expression with max consistency metric
(maxConsistency, optimalBDD) = maximumBy (comparing fst) consistencyMetrics
in (targetNode, optimalBDD, maxConsistency))
$ nodes inferredNetwork
getOptimalBoolExpressionsPar :: BoolNetwork -> Int -> [(NodeState, BDD, Double)]
getOptimalBoolExpressionsPar inferredNetwork k = map (\targetNode ->
let inpNodes = getRegulatoryNodes targetNode inferredNetwork
consistencyMetrics = searchUpdateRulePar inpNodes targetNode k
(maxConsistency, optimalBDD) = maximumBy (comparing fst) consistencyMetrics
in (targetNode, optimalBDD, maxConsistency))
(nodes inferredNetwork)
`using` parListChunk 50 rdeepseq
src/ProcessData.hs
module ProcessData
( csvToNodeStates
) where
import qualified Data.ByteString.Char8 as C
import GraphUtils (NodeState(..))
import qualified Data.Matrix as M
import qualified Data.Vector as Vec
-- Get CSV Data
-- Return (header, values as multi-D list)
getCSVData :: String -> IO ([String], [[Int]])
getCSVData fname = do
inp <- C.readFile fname
let inpLines = C.lines inp
case inpLines of
[] -> error "Invalid csv file."
[_] -> error "Invalid csv file."
(header:csvLines) -> do
let headerFormatted = map C.unpack (C.split ',' header)
csvLinesFormatted = map (map (\l2 -> read (C.unpack l2) :: Int) . C.split ',') csvLines
return (headerFormatted, csvLinesFormatted)
{-
Params:
- x: csvData returned by getCSVData
- axis: 0 = row, 1 = column
-}
parseCSVData :: IO ([String], [[Int]]) -> Int -> IO [NodeState]
parseCSVData x axis = do
csvData <- x
let (header, csvList) = csvData
csvMatrix = M.fromLists csvList
nodeStates = foldl (\acc (i, hName) -> acc ++ [NodeState hName (Vec.toList $
if axis == 0
then M.getRow i csvMatrix
else M.getCol i csvMatrix
)])
[]
$ filter (\(_, n) -> n /= "time") (zip [0..] header)
return nodeStates
{-
Params:
- fname: csv filename
- axis: 0 = row, 1 = column
Example:
t <- csvToNodeStates "../../test2.csv" 1
-}
csvToNodeStates :: String -> Int -> IO [NodeState]
csvToNodeStates fname = parseCSVData (getCSVData fname)
src/generate_data.py
# Generate large test samples
"""
Main script for generating random large datasets of input/output gene expression samples
"""
import random
import pandas as pd
import numpy as np
import argparse
def generate_io_pairs(num_nodes, time):
nodes = ["v" + str(i) for i in range(1, num_nodes + 1)] + ["v" + str(i) + "'" for i in range(1, num_nodes + 1)]
state_series = []
inp_seen = []
out_seen = []
for t in range(1, time + 1):
rand_states_inp = [random.randint(0, 1) for _ in range(num_nodes)]
rand_states_out = [random.randint(0, 1) for _ in range(num_nodes)]
inp_done = False
out_done = False
while not (inp_done and out_done):
if rand_states_inp not in inp_seen:
inp_seen.append(rand_states_inp)
inp_done = True
else:
rand_states_inp = [random.randint(0, 1) for _ in range(num_nodes)]
if rand_states_out not in out_seen:
out_seen.append(rand_states_out)
out_done = True
else:
rand_states_out = [random.randint(0, 1) for _ in range(num_nodes)]
state_series.append(rand_states_inp + rand_states_out)
state_series_df = pd.DataFrame(state_series, columns = nodes)
return state_series_df
def generate_data_time_series(num_nodes, time):
nodes = ["v" + str(i) for i in range(1, num_nodes + 1)]
state_series = []
states_seen = []
for t in range(1, time + 1):
# Ensure that simultaneous gene expressions are not repeated
rand_states = [random.randint(0, 1) for _ in range(len(nodes))]
while True:
if rand_states not in states_seen:
states_seen.append(rand_states)
break
else:
rand_states = [random.randint(0, 1) for _ in range(len(nodes))]
state_series.append([t] + rand_states)
state_series_df = pd.DataFrame(state_series, columns = ["time"] + nodes)
return state_series_df
def output_data_to_file(state_series_df, fname):
state_series_df.to_csv(fname, index=False)
print("Printed data to {}".format(fname))
def parse_args():
parser = argparse.ArgumentParser()
parser.add_argument("--numNodes", type=int, help="Number of nodes")
parser.add_argument("--time", type=int, help="Length of time-series")
parser.add_argument("--outputFile", help="Output file")`
args = parser.parse_args()
return args
# Example: python generate_data.py --numNodes 100 --time 300 --outputFile "test.csv"
if __name__ == "__main__":
args = parse_args()
data = generate_data_time_series(args.numNodes, args.time)
print(data)
output_data_to_file(data, args.outputFile)